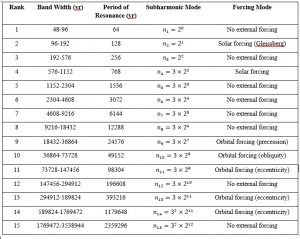
Subharmonic modes

Subharmonic modes around the subtropical gyres

Rossby waves that propagate in the oceans, either in the tropics (along with Kelvin waves) or at mid-latitudes are resonantly forced. In other words, these waves respond selectively according to the period of the forcing: the efficiency is maximum when the latter coincides with a natural period of the Rossby waves.
Gyral Rossby waves circle around the North and South Atlantic gyres and around the Indian Ocean gyre in 64 years, in 128 years around the North and South Pacific gyres. Rossby wave resonance occurs in subharmonic modes as shown in the table (for waves winding around subtropical gyres). They are obtained recursively, any mode being deduced from the previous one by multiplying it by 2 or 3, which corresponds to an optimum stability of the gyral Rossby waves. This multiplying factor is deduced from long time series of climate (ice and sediment cores).

Subharmonic modes of Gyral Rossby Waves. Their natural periods are obtained by multiplying the nth subharmonic mode (number of turns performed by the Gyral Rossby Waves around the North and South Atlantic gyres, and the Indian Ocean gyre) by 64 years (48 years before the Mid-Pleistocene Transition). The number of turns must be divided by 2 in the North and South Pacific gyres.