Contents
Kelvin waves
If William Thomson, better known as Lord Kelvin, born in Belfast in 1824, is famous for introducing the « absolute zero » of the temperature scale corresponding to the absolute absence of thermal agitation, this British physicist is not less renowned for his work in fluid dynamics. Kelvin conceptualized in 1879 the existence of an ocean wave that results from both the Coriolis force due to the rotation of the Earth and the reaction against a topographic boundary such as a coastline. The Kelvin wave also has the property of being trapped along the equator, due to the vanishing of the Coriolis force, and propagates eastward. This same phenomenon occurs in the atmosphere.
A very important characteristic of a Kelvin wave is that it is non-dispersive, i.e. its phase velocity c is constant, whatever the wavelength: it varies between 2.3 m/s and 2.8 m/s for the first baroclinic mode, depending on the oceans. In a stratified ocean, the various baroclinic modes result in the oscillation at the interfaces of layers of different densities, producing waves whose phase velocity decreases with the depth of the interface: the maximum speed corresponds to the first baroclinic mode, i.e. the oscillation of the thermocline.
Rossby waves
Carl-Gustaf Arvid Rossby born in Stockholm in 1898, a Swedish meteorologist then naturalized American, was the first to explain the large scale motions of the atmosphere through the fluid mechanics. In the 20’s, he studied hydrodynamics, the general circulation of the oceans and the atmosphere. As Rossby waves are easy to observe in the atmosphere because they form large-scale meanders of the jet-stream in mid-latitudes, ocean waves have been observed at the advent of satellite oceanography, although conceptualized as early as 30’s. Also known as planetary waves as they owe their origin to the shape and rotation of the earth, it is the crucial difference between the horizontal scale (of the order of hundreds or even thousands of kilometers) and vertical (a few centimeters) of these waves that makes them so difficult to observe. In addition, very often they take the form of solitary waves (with one peak or one trough).
Another important feature is that Rossby waves are trapped by the equator, but unlike Kelvin waves, they propagate westward or cyclonically along the subtropical gyres. Their propagation speed of a few m/s, decreases as the latitude increases. This means that at mid-latitudes the wave can take months – even years – to cross the Pacific Ocean. The solutions of the equations of motion of Rossby waves at low frequencies and long wavelengths are non-dispersive, hence the propensity of these waves to cross the oceans without distortion.
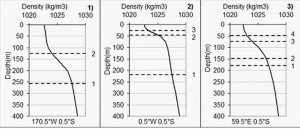
Pycnocline
The pycnocline is the layer where the density changes rapidly with depth. It results from the stratification under the effect of gravity of the mixed layer. In tropical oceans, the base of the pycnocline coincides with the thermocline where the temperature changes rapidly with depth. The top of the pycnocline is at the interface between the surface water, of low density, and the stratified layer.
Thermocline
The thermocline is the zone of steep thermal transition between surface and deep waters. In the seas and oceans, almost all the sunlight striking the surface is absorbed by the surface layer of water which then heats. The wind and waves move the water, distributing heat so nearly uniform on the first tens of meters deep. If convection or mixing are low, the upper layer, less dense and warmer, floats on the cold underlying layer. Through this thin transition zone that is the thermocline, the temperature drops very quickly, by 20°C in tropical oceans. Below the thermocline, the temperature continues to drop with depth but much slower.
Solar forcing tends to move the thermocline up and down to the rhythm of different cycles: it deepens during a phase of high solar activity when surface water warms. In contrast it rises when solar activity wanes because the thickness of the warm surface layer is reduced as resulting from an unbalance between incoming and outgoing fluxes. A positive feedback is exerted on the polar current around the gyre, whose velocity is proportional and in phase with the oscillation of the thermocline: the excess heat transported to the pole resulting from the acceleration of the western boundary current favors the deepening of the thermocline, which further increases the speed of the polar current (therefore the western boundary current).
Baroclinic modes
The solution of the equations of motion shows several vertical baroclinic modes that are established according to the pycnocline, i.e. the distribution of the density of seawater as a function of depth. In a stratified ocean, the interface between two layers is subject to an oscillation phenomenon whose natural (normal) frequency depends on the difference in buoyancy between the two layers. Each interface corresponds to a phase velocity of baroclinic waves travelling horizontally.
The density increases with depth, the densest water naturally being in the ocean depths. However, the evolution of density with depth is not uniform. In equatorial and tropical regions, there is a layer of water near the surface of almost constant density, then a transition zone through which the density increases very rapidly with depth. This layer so-called pycnocline generally coincides with the thermocline. To larger depths the density changes slowly. At high latitudes, the density of the layer near the surface is high because of the low temperature of seawater; the vertical profile is less contrasted and pycnocline less easy to discern.
The distinction between different normal modes is therefore at low latitudes. For the first baroclinic mode, the interface is at the base of the pycnocline, which at the equator is in average at 255 m in the Pacific Ocean, 220 m in the Atlantic Ocean and 180 m in the Indian Ocean. The phase velocity measured in the Pacific is about 2.8 m/s; so an equatorial Kelvin wave takes two months to cross the Pacific from New Guinea to South America. The phase velocities are measured to 2.35 m/s and 2.30 m/s in the Atlantic and Indian Oceans. The surface height perturbation η corresponding to this mode of propagation reflects changes in depth of the thermocline, but opposite in sign and approximately 300 times lower: an elevation of 5 cm of the surface corresponds to a deepening of the thermocline of about 15 m.
The interface of another important mode is at the top of the pycnocline, i.e. in average at 125 m, 30 m and 50 m in the Pacific, Atlantic and Indian oceans, respectively, with phase velocities of 1.0 m/s in the Pacific and 0.28 m/s in the other two oceans. Other intermediate modes can be identified, probably resulting from coupling with the two main modes.
Meridional modes
If the vertical baroclinic modes are resulting from the stratification of the oceans, meridional (latitudinal) modes of Rossby waves reflect the effects of the variation of the Coriolis parameter ƒ. For this reason these modes result from what is called the dispersion β where β represents the variation of the Coriolis parameter with respect to the latitude. The Coriolis parameter or Coriolis frequency ƒ is defined from the speed of rotation on the surface of the terrestrial sphere, and increases with latitude. This parameter is zero at the equator and reaches its maximum at the poles.
There are different modes of propagation of Rossby waves, which differ in their latitudinal structure. This is why they are called meridional modes. For the first baroclinic mode, the phase velocity of the first meridional mode equals c/3. In other words, the first meridional mode Rossby waves propagate three times slower than the Kelvin waves (and in the opposite direction). On the other hand the waveform is symmetrical about the propagating direction.
The phase velocity of the second meridional mode equals c/5 and the wave is anti-symmetric with respect to the direction of propagation. When the meridional mode increases the phase velocities decrease from c/7 to c/9… The waves whose mode is odd are symmetrical, those whose mode is even are anti-symmetric. The meridional structure becomes complex when the mode increases as the amplitude of the wave vanishes and changes sign periodically. Unlike baroclinic modes whose amplitude decreases with the mode, interfaces becoming shallower, meridional modes of high order may be of large amplitude when they are resonantly forced, as is the case in the tropical Pacific. In solving the equations of motion, the forcing terms indeed depend on the meridional mode considered. Wind stress, for example, does not act the same way on the first meridional mode, which is symmetrical about the equator, and the second meridional mode, which is anti-symmetric.
Glossary
In a homogeneous medium, propagation in a given direction of a monochromatic wave (or sine) results in a simple translation of the sinusoid at a speed called phase velocity or celerity. In a non-dispersive medium, the speed does not depend on the frequency (or wavelength). In this case every complex wave is the sum of several monochromatic waves that also undergo an overall translation of its profile, this without deformation. In contrast, in a dispersive medium the phase velocity depends on the frequency and the energy transported by the wave moves at a speed lower than the phase velocity, said group velocity.
Non-dispersive waves. They are such that the phase velocity of the ridge of the wave is equal to the group velocity of the energy carried by the wave, and this for all the frequencies (or all wavelengths). This means that the wave propagates without deformation.
Baroclinic wave. In contrast with barotropic waves that move parallel to isotherms, baroclinic Rossby or Kelvin waves cause a vertical displacement of the thermocline, often of the order of several tens of meters. The seconds are usually slower than the first.
The Coriolis parameter f is equal to twice the speed of rotation Ω of the earth multiplied by the sine of the latitude φ: f = 2Ωsin φ. The Coriolis force, on the other hand, is perpendicular to the direction of movement of the moving body. It is proportional to the velocity of the body and the speed of rotation of the medium.
Positive feedback loops amplify changes in a dynamic system; this tends to move the system away from its equilibrium state and make it more unstable. Negative feedbacks tend to dampen changes; this tends to hold the system to some equilibrium state making it more stable.