Contents
Radiative forcing
The greenhouse effect (or radiative forcing) is due to the low temperature of the upper layers of the troposphere, compared with the temperature of the surface of the earth. The earth-atmosphere system would not know, in fact, the greenhouse effect if it were isothermal, emitting as a whole in the infrared spectrum as would a black body.
The greenhouse effect increases the planet’s surface temperature by reducing energy loss to space whose temperature is close to absolute zero (2.7 K) by absorption of infrared emitted by the earth. This absorption mainly results from water vapor in the lower layers of the atmosphere, warm and humid, and from CO2 in the upper layers, cold and dry.
The role of greenhouse gases such as methane (CH4) or ozone (O3) is well understood, the absorption of infrared emitted from the earth’s surface in the absorption bands of these gases directly depending on their concentration in the atmosphere. On the other hand, this causal relationship is more subtle for CO2 because of saturation phenomenon so that, under a first approximation, absorption does not increase with concentration. But this is not entirely true for two reasons:
- CO2 absorption line between 14 and 17 µm is not saturated in the side band: absorption thus increases weakly with CO2 concentration
- Altitude from which the thermal radiation escapes to space increases with the concentration of CO2 because of the thickening of the opaque layer in which any emission in the infrared spectrum of CO2 is reabsorbed or scattered. The temperature decreases with altitude, the emission is lower, which increases the radiative forcing of the atmosphere.
It is necessary to emphasize the special role played by water vapor on climate: the mechanism invoked to explain the warm weather on our planet, which should be -18 ° C in the absence of any greenhouse effect, is mainly attributed to it. In contrast, the thermal convection redistributes moisture and homogenizes the temperature in the layer from 0 to about 4.4 km. This influences the vertical thermal balance of the planet by reducing the average decrease in temperature with altitude that the greenhouse effect imposes to the troposphere. Without convective mechanisms, the change would be steeper and give a higher average temperature of the earth’s surface. By evaporating from the oceans water vapor draws energy, the latent heat, which is released during its condensation in the atmosphere. The resulting warming limits the convection from the surface of the earth, reducing heat exchange into the upper atmosphere. Added to this is the action of low clouds that have a high albedo effect and high clouds whose greenhouse effect is substantial.
Energy balance
The link between global warming and the increasing concentration of atmospheric carbon dioxide since the beginning of the industrial age is poorly understood. A positive feedback from water vapor as a result of temperature increase amplifies the impact of greenhouse gases. The feedback loop involves the oceans both as a source of water vapor and as a moderator of the surface temperature of continents. On the other hand, anthropogenic warming is superimposed on the natural variability of the climate, which until now has remained highly speculative.
At thermal equilibrium, the solar energy received by the earth is equal to the thermal energy re-emitted into space as infrared radiation. By writing that the infrared flux emitted = Solar Flux absorbed, we obtain the well-known relationship:
4πR2σTe4= (1-A) πR2F0
where 4πR2 represents the surface of the earth, σTe4 the emission of black body, (1-A) the absorption coefficient, πR2 the earth section, and F0 the solar flux outside the atmosphere; Te is the radiative equilibrium temperature, A the planetary albedo, and σ the Stefan-Boltzmann constant (5.67.10-8W.m-2 .K-4).
To quantify the effect of radiative forcing on the global average temperature, assume at first a perfectly transparent atmosphere to thermal radiation re-emitted by the earth. In this case, the emitted radiative power σTe4 would balance exactly the incident radiative power of solar shortwave radiation actually reaching the surface of the earth (1-A)F0/4, i.e. 240 W/m2 (F0 =1365.8 W/m2, the current albedo is close to 0.3), which gives Te=-18°C (255 K).
The mean global temperature of the earth is 15 °C (288 K), which corresponds to a radiative power equal to σTe4 = 390 W/m2. The difference between this radiative power and what would be emitted in the absence of atmosphere is 390-240= 150 W/m2, corresponding to the absorption by the real atmosphere in the presence of water vapor, greenhouse gases, clouds and aerosols. The radiative forcing efficiency is then (288-255)/150 = 0.22 °C/(W/m2).
Warming and anthropogenic CO2
Thermal radiation in the CO2 absorption band
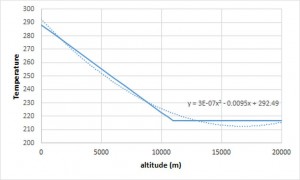
Knowing the radiative forcing efficiency, let’s estimate the impact on the global temperature of a change in the concentration of atmospheric CO2 by involving thermal radiation in the CO2 absorption band between 630 and 700 cm-1. When the concentration increases the altitude from which the thermal radiation is emitted toward the cosmos also increases. As shown in the table representing the partial CO2 pressure (product of the pressure by the concentration) as a function of altitude for concentrations of 300, 400 and 500 ppmv, the temperature of the emitted radiation can be determined using the » normal temperature and pressure « (NTP) which allow to overcome the variations of these two parameters depending on location and time considered. The NTP pressure is expressed by the equation P=1013.25 x (1-0.0065 x z/288.15)5.255 where z is the altitude (m). At the sea level the pressure is 1013.25 hPa, the temperature 15 °C and the lapse rate -6.5 °C/km. To 11 km altitude the pressure drops to 226.38 hPa and the temperature to -56 °C. Between 11 km and 20 km (stratosphere) the temperature remains constant. In order to overcome the singularity of temperature at 11000 m resulting from the equation change, an adjustment by a second order polynomial is performed.
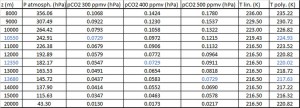
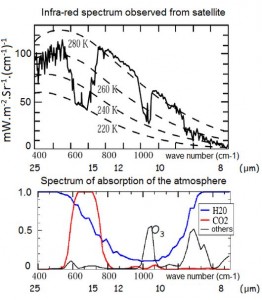
Considering thermal radiation corresponding to 400 ppm of CO2, the emitted radiative power derived from the satellite observed infrared spectrum, reduced to the terrestrial sphere, is 38.55/4=9.64 W/m2 to a temperature equal to 220 K, which corresponds to an altitude of 12350 m and a CO2 partial pressure of 0.0729 hPa.
Now we can deduce what was the radiative power emitted at the beginning of the industrial age when the CO2 concentration was 300 ppmv, which corresponds to a 10550 m altitude emission and a temperature of 224.93 K. Application of Stefan-Boltzmann’s law gives 9.64 x (224.93/220)4 = 10.53 W/m2, i.e. a power gain of 10.53-9.64 = 0.89 W/m2. This corresponds to a decrease in temperature of 0.19 °C from the radiative forcing efficiency.
In terms of the climatic impact in the case of doubling the concentration of anthropogenic CO2, a concentration of 500 ppmv corresponds to a 13680 m altitude emission and a temperature of 217.63 K. The re-emitted radiative power derived from the Stefan-Boltzmann’s law is 9.64 x (217.63/220)4 = 9.23 W/m2, i.e. a power loss of 9.64-9.23 = -0.41 W/m2, which corresponds to a temperature increase of 0.09 ° C.
Effect of broadening of the CO2 absorption band
To anthropogenic warming resulting from increasing altitude from which the thermal radiation escapes to the cosmos adds the effect of the broadening of the CO2 absorption line when the concentration of carbon dioxide increases. If an atmosphere of average humidity is considered, the increase, since the beginning of the industrial era, of radiative forcing ∆e (W/m2) resulting from radiation re-emitted to the earth in the band 14 – 17 µm is expressed, depending on the relative content of CO2 compared to what it was in 1850, i.e. (CO2)/(CO2)1850 , by the relationship:
∆e=2.94*Log2 [(CO2)/(CO2)1850]
Anthropogenic warming deduced from the instrumental global temperature (Pinault, 2018e)
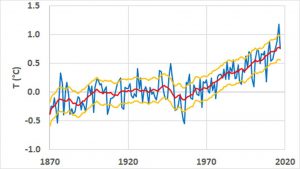
The actual contribution of anthropogenic warming to observed global warming can be estimated relatively accurately by deducting from the instrumental global temperature the natural variation of the temperature deduced from the measurement of the sea surface temperature at specific locations of sub-tropical gyres representative of long-term heat exchanges between oceans and continents (see « climate change« ).
The anthropogenic contribution to the global temperature is obtained by subtracting the oceanic signal from the instrumental surface temperature. Significant variations are observed before 1970, mainly due to a lack of representativeness of the areas selected to estimate the contribution of each of the oceans to the variability of the climate from the average temperature of the surface of the seawater. The anthropogenic component of the global temperature has increased linearly since 1970 without any inflection. The global warming seems close to 0.8 ° C in 2017.
This estimate is higher than the increase in Tmg resulting from the increase in altitude from which thermal radiation escapes to the cosmos, which is close to 0.30 ° C. This bias results from the high troposphere cloud cover, which involves the lapse rate, surface albedo and cloud feedbacks. Carbon dioxide contributes about 80% to radiative forcing due to greenhouse gases.
References
Clive Best, Doubling CO2 and basic physics, http://clivebest.com/blog/?p=1169
Hanel R.A., B. Schlachman, D. Rogers, D. Vanous, The Numbus 4 Michelson interferometer, Appl Opt. 1971 Jun 1;10(6):1376-82. doi: 10.1364/AO.10.001376.
IPCC Fifth Assessment Report – Climate Change 2013 – www.ipcc.ch/report/ar5/wg1/
Dufresne J-L and Treiner J. (2011) L’effet de serre atmosphérique : plus subtil qu’on ne le croit !, http://www.udppc.asso.fr/bupdoc/consultation/article-bup.php?ID_fiche=21046 (in French)
Anthony Watts, The Logarithmic Effect of Carbon Dioxide, http://wattsupwiththat.com/2010/03/08/the-logarithmic-effect-of-carbon-dioxide/
ERBE (The Earth Radiation Budget Experiment) NASA program, 1996, FS-1996-05-03-LaRC, http://www.nasa.gov/centers/langley/news/factsheets/ERBE.html
Gill AE (1982) Atmosphere–Ocean Dynamics, International Geophysics Series, 30, Academic Press, 662 pp.
Kallberg, P., Berrisford, P., Hoskins, B., Simmons, A., Uppala, S. and Lamy-Thepaut, S (2005) ‘Atlas of the atmospheric general circulation’. ECMWF ERA-40 Project Report Series, No. 19. European Centre for Medium-Range Weather Forecasts, Shinfield, Reading, UK (available from www.ecmwf.int/publications)
Trenberth K. E., J. T. Fasullo, and J. Kiehl (2008) Earth’s Global Energy Budget, American Meteorological Society, DOI:10.1175/2008BAMS2634.1
Zhou, Y., D. P. Kratz, A. C. Wilber, S. K. Gupta, and R. D. Cess (2007), An improved algorithm for retrieving surface downwelling longwave radiation from satellite measurements, J. Geophys. Res., 112, D15102, doi:10.1029/2006JD008159.
Glossary
The latent heat is heat-exchanged in the change of state of the seawater during the process of vaporization.
A black body in thermal equilibrium (that is, at a constant temperature) emits electromagnetic radiation called black-body radiation. The radiation is emitted according to Planck’s law, meaning that it has a spectrum that is determined by the temperature alone, not by the body’s shape or composition. For example the Sun can be considered as emitting black-body radiation that exhibits a distribution in energy characteristic of the temperature T=5780 K: the photosphere contains photons of light nearly in thermal equilibrium, and some escape into space while producing negligible effect upon the equilibrium of the radiation inside the photosphere.
Escaping radiation from the earth also approximates black-body emission that exhibits a distribution in energy characteristic of the temperature T=288K. Photons whose energy corresponds to the saturated absorption bands of the atmosphere (water vapor, CO2) are also in thermal equilibrium if they escape from the opaque layer: the temperature gradually decreases with altitude in the troposphere (-6.5°C/km).
The albedo, which is the ratio of solar energy reflected by a surface to the incident solar energy is high on the polar caps (about 60%) and much lower on the oceans (5-10%). For a period of cooling the polar caps extend, increasing the albedo. The planet reflects more solar radiation, absorbs less, which enhances cooling. Warming has the opposite effect: the global warming melts the polar ice, which reduces the albedo and thus increases the temperature of the planet.
The adiabatic lapse rate is, in the Earth’s atmosphere, the variation of air temperature with altitude (in other words, the gradient of the air temperature). Adiabatic means that a mass of air does not exchange heat with its environment (other air masses, relief). If we exclude condensation (formation of clouds and precipitation) and vaporization, the lapse rate of the atmosphere depends only on the pressure.
The absorption bands of the infrared radiation emitted from the surface of the earth are saturated when the optical length is much less than the thickness of the absorbent layer of the atmosphere. In this case, the layer is opaque and the emission is reduced to diffuse radiation (thermal radiation) from its surface.